Volume8 No.2

背景と研究目的：

　銅及び銅合金は電気特性と強度特性のバランスに優れ、電線用導体や端子材に最適な材料である。例えば自動車の内部配線に用いられる電線の場合、電動化の進展に伴って配線本数が増加しており、電線総重量の維持もしくは低減のためには導体の細径化が必須となる。これには従来以上の高強度と高導電率の両立が必要であり、加工変形における原子レベルの構造変化の理解が非常に重要である。近年、放射光を用いて実施された「引張その場 XRD」は、これを実現するものとして高い注目を浴びている[1]。ここで配向を含めた銅材全体の評価には透過法を用いる必要があるが、本研究の対象である銅材の場合、透過能のために測定効率に課題があった。具体的に端子材の厚みを想定してみると、300 µm の純銅板に対するX線透過率は 20 keV の場合に 0.01% しかないが 37 keV の場合に 20% となるため、短時間で測定するためには高エネルギーが望ましい。一方で 20 keV を超える高エネルギーでは、汎用的な二次元検出器で用いられる Si 素子では検出感度が大幅に低下する。そこで今回は、高エネルギーでも十分な感度を有する CdTe 素子の二次元検出器を用い、実際の製品厚みで高効率その場解析を試行し、有効性を検証した。なお測定対象として当初は線材を測定する計画としていたが、今回用いた試験機では、引張に伴い線材が引張方向と垂直方向へ最大 100 µm 程度変位して試料がビームの強度中心から外れ、測定困難となることが判明した。このため計画を変更し、変位方向に対して試料が十分に大きい板材を対象に実施した。

実験：

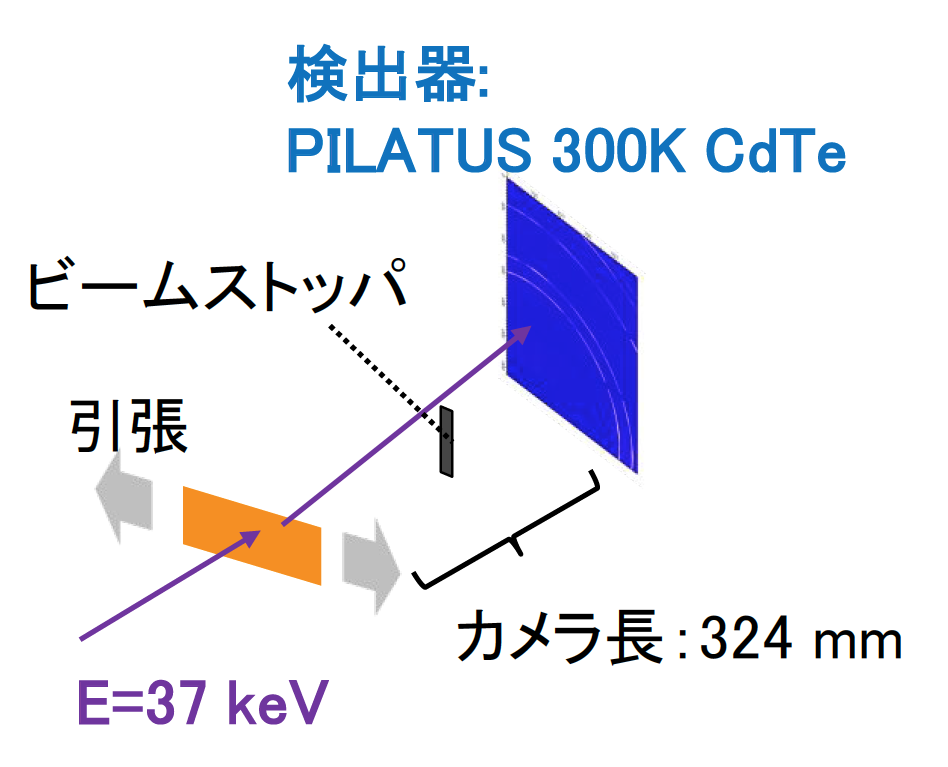
　実験は BL16XU (サンビームID) にて図１の配置で実施した。Si 111 二結晶分光器で 37 keV（～Si111 上限）に単色化した放射光を、Rh コートミラー（入射角 1.5 mrad）で高次光を除去し、開口 0.2 mm 角の四象限スリットで整形し、試料に照射した。検出器にはPILATUS 300K CdTe (Dectris 製)を用い、検出面を入射ビームと垂直向きに設置し、Debye ring の 1/4 以上の方位角を含むように調整した。試料と検出器の距離は 324 mm で、CeO₂ (NIST 674a) の Debye ring から、Fit2D[2]を用いて算出した。なお二次元検出器像は分割ヒストグラム法[3]を用いて一次元化し、1ピクセル辺りの強度で比較を行った。

　　　　　　　　　　　　　　　図１. 引張その場 XRD の実験配置

　試料には 300 µm 厚の純銅板（純度 99.99%）を真空雰囲気で 250°C、1 h の熱処理で軟化させたものを用いた。引張試験機には Linkam 製 10073B を用いた。試料は短冊状に切断し、初期長さ 15 mm から歪速度 1×10^-3 /s で圧延方向と平行な向きに引っ張った。露光は 1 s 間隔で連続的に実施し、試料の変位 1% あたり10回の測定を行った。

結果および考察：

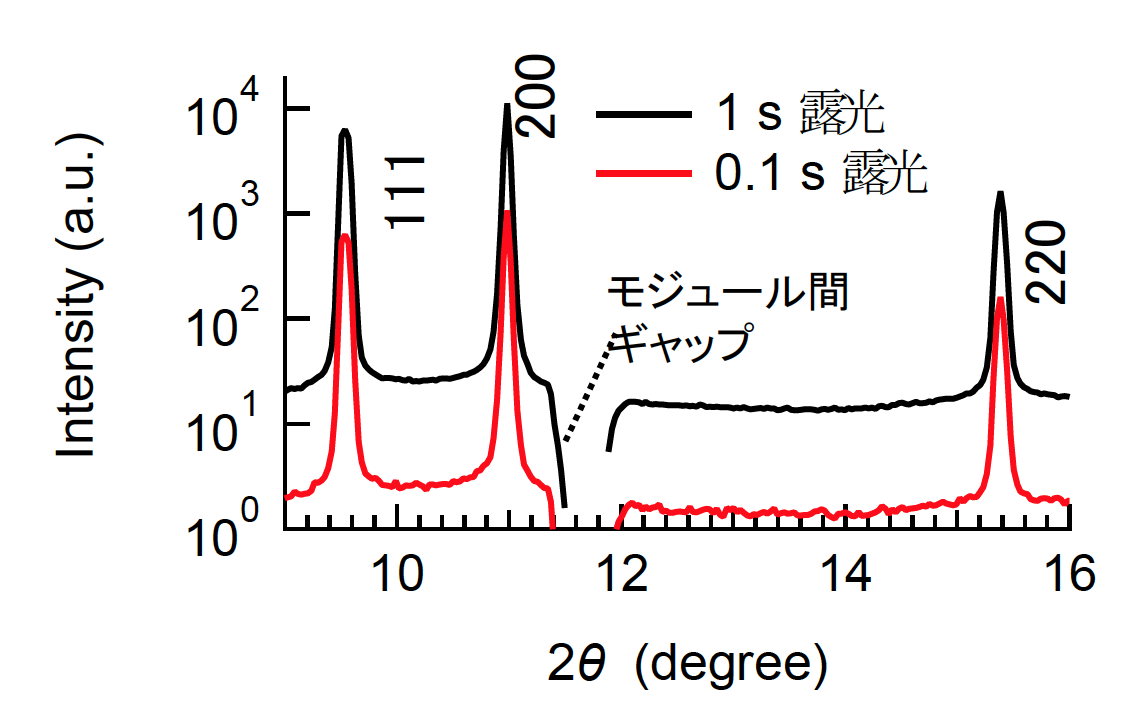
　はじめに露光時間の検証を実施した。図２に露光時間 0.1 s で測定した二次元像、図３に 0.1 s、1 s で測定した二次元像を引張と垂直方向（方位角 ±10°）で一次元化したプロファイルを示す。0.1 s 露光でも S/N に大きく遜色なく、議論に十分なデータが得られていることが分かる。この結果は、比較的速い歪速度でも 0.1 s 程度の十分な時間分解能で測定が可能であることを示している。なお二次元像から、Debye ring の強度分布は配向に由来する強度差が概ね連続的に見えているが、図２の赤破線内には不連続的な輝点が観測されており、一部粗大粒が混入していることが明らかになった。一方で図３の通り、一次元像では対数スケールで見る限りは明らかな不連続等の粗大粒の影響は見受けられなかった。

　　　　図２. 露光時間 0.1 s で測定した二次元像の例。赤枠内の輝点は粗大粒の影響。

　　　　　図３. 図２を引張と垂直方向（方位角 ±10°）の範囲で一次元化した XRD プロファイル。

　　　　　　　　　　　　　　　　黒線は 1 s 露光、赤線は 0.1 s 露光

　次に、露光時間 1 s で行った引張その場測定の結果について示す。図４(a)は荷重変位曲線であり、2% 付近で弾性変形域から塑性変形域へ変化し、6% 付近で破断が起こっている。図４(b)に約 1% 置きに得た二次元画像から引張方向（方位角 ±10°）で一次元化した 200 回折線の生データ、及び分割擬 Voigt 関数[4]でフィッティングした曲線を示す。弾性変形域である 0% から 2% の間で大きなピークの低角側へのシフト、即ち面間隔の拡大が見られている。これは外力に対応したものであると考えられ、弾性変形域を過ぎた 4% 以上では変化はほとんど見られなくなっている。図４(c)に引張と垂直方向（方位角 ±10°）の 200 回折線の変化を示す。引張方向と同様に 2% 程度までピークシフトが見られるが方向は高角側、即ち面間隔が縮小する方向であり、これは引張方向の膨張にポアソン比の分だけ収縮したものと考えられる。なお 3% 以降については少し低角側に戻るような挙動も見られている。

　　　図４. (a)荷重変位曲線、 (b)引張方向及び(c)引張と垂直方向の200回折線変化の抜粋。

　　　　　　　　　点は生データ、実線は分割擬 Voigt 関数によるフィット曲線

　図５、図６、図７に 111、200、220 回折線の回折角及び積分幅を示す（220 回折線の引張方向は測定範囲外）。なお回折角はピークトップを示す 2θ 値、積分幅はピーク面積からピークトップにおける高さを割り算して算出した[5]。回折角については、図４(b)及び(c)で定性的に把握した傾向と合致しており、弾性域で、膨張及び収縮に対応したピークシフトが見られ、塑性域では変化が穏やかになっている。また、図４(c)のように同一方向ではなく逆方向への動きも見られている積分幅については結晶子サイズや不均一歪の変化に対応し、塑性変形量の増加に従って増加していくべきであるが、特に図５(b)や図６(b)、図７(b)では不規則に増減を示している。これらのピーク位置及び積分幅の不規則な挙動は、図２の二次元像でも見られた粗大粒の影響を受けている可能性があり、引張によって粒子が平行移動や回転することで、ビーム照射領域内で回折条件を満たす粗大粒が変化していったものと考えられる。

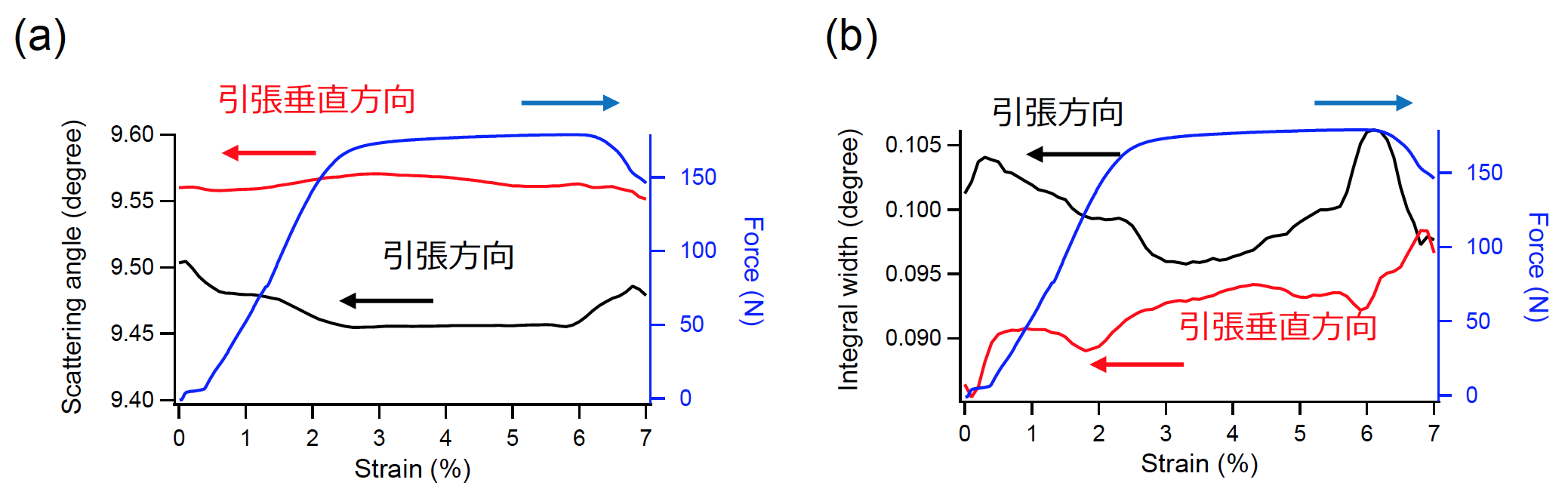
　　図５. 111 回折線の(a)ピーク位置及び(b)積分幅の歪に対する変化。青線は荷重曲線（右軸と対応）

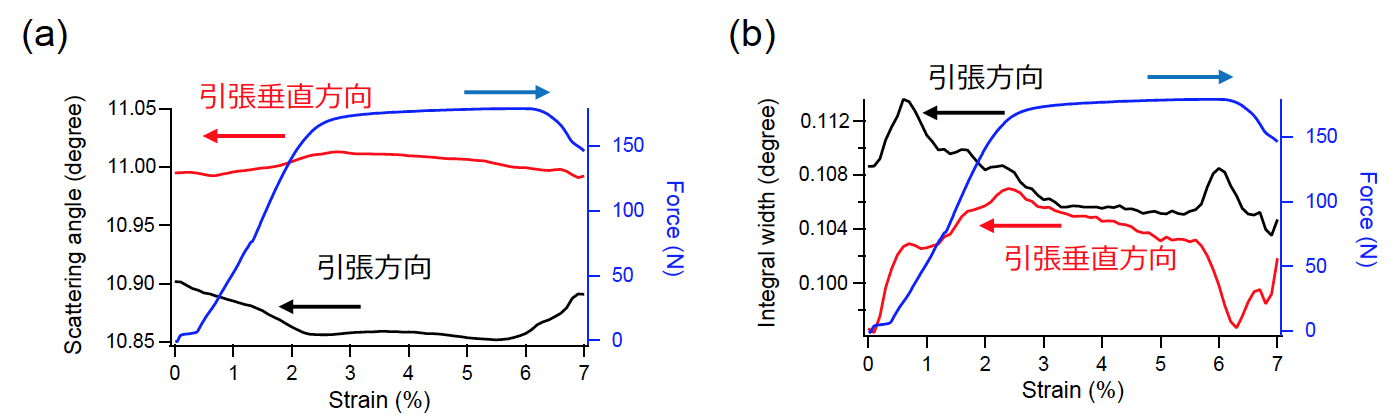
　　図６. 200 回折線の(a)ピーク位置及び(b)積分幅の歪に対する変化。青線は荷重曲線（右軸と対応）

　　図７. 220 回折線の(a)ピーク位置及び(b)積分幅の歪に対する変化。青線は荷重曲線（右軸と対応）

まとめ及び今後の課題：

　今回の実験条件では、厚み 300 µm の純銅板を対象に短い露光時間で、配向やピーク位置変化（面間隔の膨張や収縮）が捉えられることが明らかになり、CdTe 素子の二次元検出器の有用性が確認できた。一方で粗大粒の影響を大きく受けており、このような条件では結晶子サイズや不均一歪（もしくは転位密度）の算出は困難である。このため、試料を引張試験機ごと揺動し、実効的な照射面積、及びそれに含まれる粒子数を増やす等の対策を実施していく予定である。

参考文献：

[1] H. Adachi et al., Mater. Trans. 56, 671 (2015).

[2] A. P. Hammersley et al., High Press. Res. 14, 235 (1996).

[3] 藤久裕司、高圧力の科学と技術、15, 29 (2005).

[4] H. Toraya, J. Appl. Crystallogr. 23, 485 (1990).

[5] 早稲田嘉夫、 松原 英一郎、X線構造解析、 内田老鶴圃, 1998, 122.

(Received: November 11, 2019; Early edition: February 27, 2020; Accepted: July 6, 2020; Published: August 21, 2020)