Volume8 No.1

背景と研究目的：

　窒化物系半導体レーザは、高密度光記録システムであるブルーレイディスクレコーダの光源として開発され、現在では、レーザディスプレイ、プロジェクタや自動車のヘッドライト等の光源にも利用され始め、より高出力・高効率化が求められている。その解決法の１つは、デバイスの抵抗を決めている p 型結晶の低抵抗化と p 型コンタクト比抵抗の低減である。

　これまでに、GaN 中の III 族元素である Ga の一部を In に置き換えた窒化物系混晶半導体である Ga_1-xIn_xN に Mg アクセプターを添加することで、p 型結晶の低抵抗化[1,2]とともに p 型コンタクト比抵抗の低減[3]が報告されている。この実験結果は、Ga_1-xIn_xN 中の Mg アクセプターの活性化エネルギーが GaN のものよりも低減できることに起因したものと考えられる。

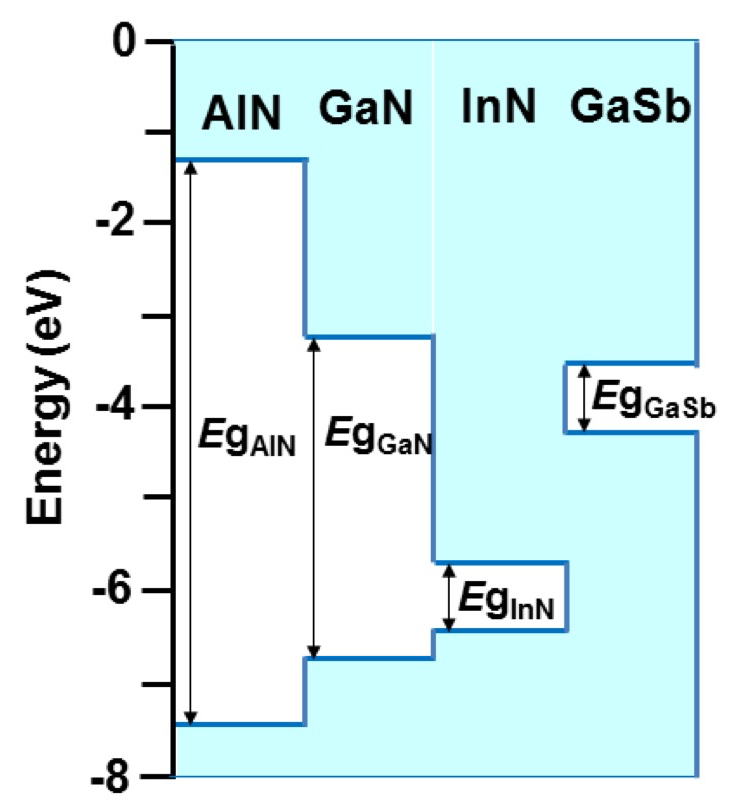
　更に、Mg アクセプターの活性化エネルギーを低減するためには、GaN 中の V 族元素である N を Sb で置換した窒化物系混晶半導体 GaN_1-xSb_x を利用することが効果的であることが、図１より予想される。なぜならば、その構成材料である GaSb の価電子帯のエネルギー上端が GaN や InN のものより真空準位に近いからである[4]。しかしながら、GaN 中の N は平衡蒸気圧が非常に高いために脱離しやすく、全組成領域にわたる GaN_1-xSb_x の結晶成長は難しい。これまでの報告によると、N-rich 領域では、分子線エピタキシー（MBE）法により Sb 組成 x= 0.04 [5]、有機金属気相成長（MOCVD）法により x=0.0005 の GaN_1-xSb_x の成長[6]が報告されていた。最近になり、竹内らは、MOCVD 法により x=0.011 までの GaN_1-xSb_x を成長し、Sb 含有率を高めるとX線回折測定で得られる平均的な格子定数が広がることを報告している[7,8]。

図１．理論計算により求められた AlN、GaN、InN、GaSb のバンドギャップ（伝導帯の下端と価電子帯の上端）のエネルギー位置の関係 [4]

　GaN_1-xSb_x を実際の光デバイスに利用するためには、含有可能な Sb 組成を高めつつ、その光学的特性を更に向上させる必要がある。これらの問題を阻害している原因の１つは、Ga-Sb のボンド長（原子間距離）（d_Ga-Sb=2.64 Å[9]）が Ga-N のボンド長（d_Ga-N=1.95 Å[10]）の 1.35 倍にも達することから相分離が起き易いことにあり、実際には、均一で理想的な構造を有する GaN_1-xSb_x 混晶半導体を実現できていない可能性がある。この問題を明らかにするには、通常のX線回折測定で得られる平均的な格子定数だけではなく、Sb 原子近傍の局所構造を明らかすることが必要であるが、これまでに報告例はない。そこで、前述のX線回折測定で構造評価をした Sb 添加 GaN（理想的な構造を有する GaN_1-xSb_x 混晶半導体ではない場合もあることから、本報告では、以降はこの表現を用いる）に対して、X線吸収微細構造（XAFS）法による測定を行い、Sb 原子近傍の局所構造を求めた。XAFS 法は上記測定のためには、大変有効な手法である。

実験：

　測定試料は、サファイア基板上に MOCVD 法で成長した GaN（厚さ 2 µm）上の Sb 添加 GaN（厚さ 500 nm）であり、SIMS 測定とともに、X線回折により平均的な格子定数を求め Sb 含有率を見積もった[10]。本実験で用いた試料は、水素キャリアガス雰囲気中で、温度 T= 800 と 950℃ で成長し、それぞれの Sb 組成は x=0.008 と 0.0015（GaN_1-xSb_x 混晶半導体が成長していることを仮定して見積もった値）と求められた。XAFS 測定は、SPring-8 のビームライン BL01B1 において、蛍光法により行った。X線の入射角を 1º に設定し、試料から発生した Sb の K_α1 及び K_α2 の蛍光X線を19素子半導体検出器（SSD）により測定した。この時、試料からの弾性散乱X線の影響を低減させるために、試料に対する19素子 SSD の配置最適化と、測定中の試料回転を行った。また、比較試料として、液体封止引き上げ（LEC）法で成長した GaSb 基板（厚さ 450 µm）を用意し、転換電子収量法により XAFS 測定を行った。

結果および考察：

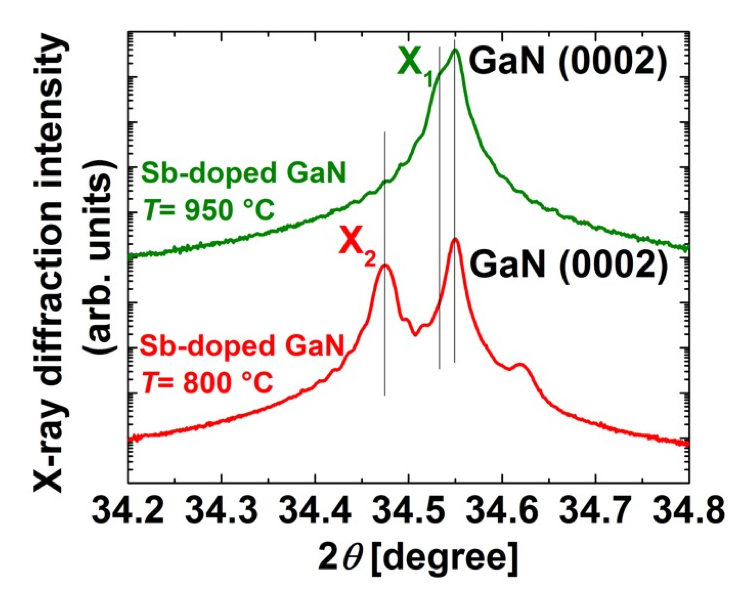
　図２に、結晶成長温度 T =950 及び 800 °C の試料に対する、それぞれのX線回折スペクトルを示した。ここでは、GaN (0002)からの回折とともに、その低角側にそれぞれ X₁ 及び X₂ の明瞭なピークが現れる。その信号のピーク位置が、結晶成長温度を T =950 から 800℃ に下げることで、より低角側にシフトする。この振る舞いは、GaN に Sb を添加することで GaN_1-xSb_x 混晶半導体が成長し、更に成長温度を下げることで、Sb 含有率が上昇し、平均的な格子定数が広がったとも考えられる[10]。しかしながら、以下に示す XAFS 測定の結果は、このモデルを否定する。

図２．T= 950 及び 800 °C で成長した Sb 添加 GaN のX線回折スペクトル。GaN(2000)からの回折とともに、その低角側にピーク X₁ 及び X₂ がそれぞれ観測される。

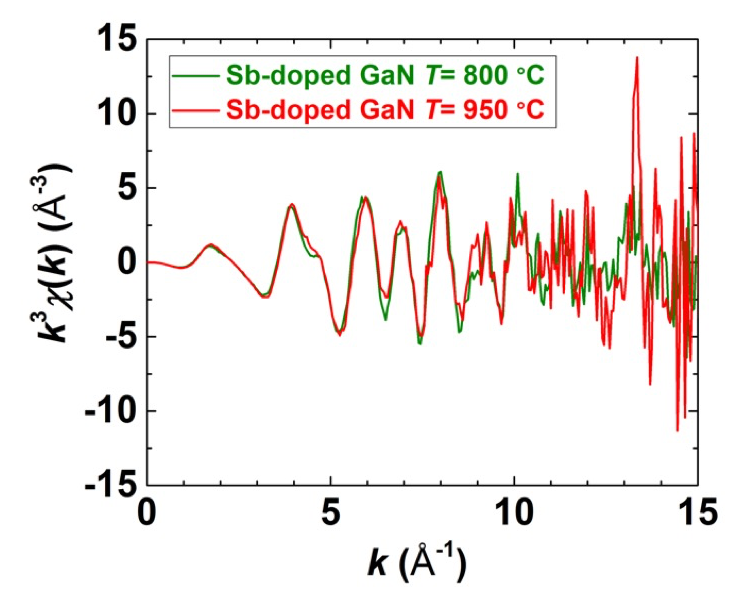
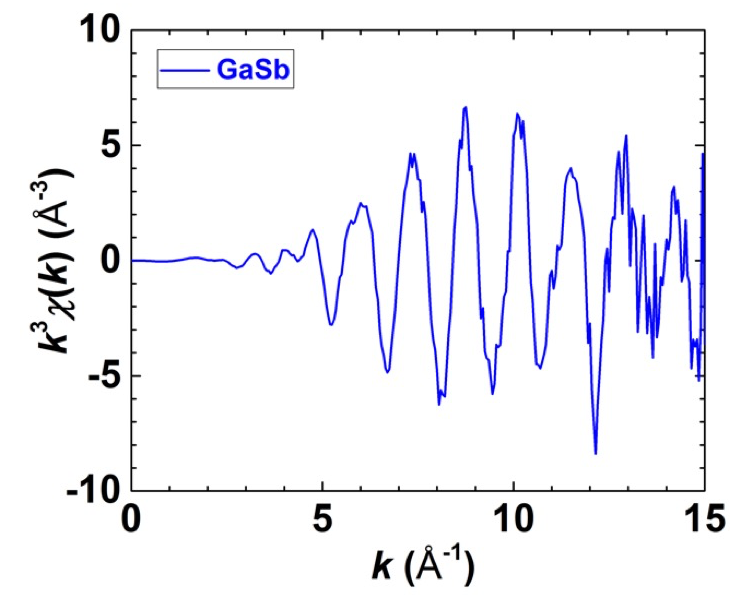
　図３に、温度 T = 950 及び 800 °C で成長した Sb 添加 GaN の Sb 蛍光 XAFS スペクトルから抽出した EXAFS 振動の波数依存性を示した。また、図４には、GaSb 基板の電子収量 XAFS スペクトルから抽出した EXAFS 振動の波数依存性を示した。図３及び図４のどちらも、縦軸には、k³（k：波数）の重みづけをした EXAFS 振動 k³χ(k)をプロットした。Sb 添加 GaN 中の Sb 濃度が、GaSb 基板のものに比べ、数100分の1程度と希薄であるが、19素子半導体検出器を使いながら積算測定を繰り返すことで、図３のようなEXAFS振動を得ることができた。

図３．T = 950 及び 800 °C で成長した Sb 添加 GaN の Sb 蛍光 XAFS スペクトルから抽出した EXAFS 振動の波数依存性縦軸には、k³（k：波数）の重みづけをした EXAFS 振動 k³χ(k)をプロットした。

図４．GaSb 基板の電子収量 XAFS スペクトルから抽出した EXAFS 振動の波数依存性縦軸には、k³（k：波数）の重みづけをした EXAFS 振動 k³χ(k)をプロットした。

　一般に、AC という２元半導体中の A 元素の一部を B 元素に置換した混晶半導体 A_1-xB_xC を考えると、その内部の A-C 及び B-C のボンド長は混晶組成に大きくは依存せず、２元半導体 AC 及び BC の本来のボンド長をそれぞれ維持し、２種類のボンド長が異なることによって発生する混晶半導体中の歪場はボンド角が変化することで緩和されていると考えられている[12]。このような特徴は、窒化物系混晶半導体である Al_xGa_1-xN [10]、Ga_1-xIn_xN [11, 13, 14]、Al_1-xIn_xN [15]でも確認されており、我々の知る限り例外はない。例えば、Ga_1-xIn_xN 内の In-N や Ga-N のボンド長は In 組成を変えても大きく変化せず、InN や GaN 中のボンド長である In-N や Ga-N をそれぞれ維持していることが分かっている。したがって、Ga_1-xIn_xN 中の In 原子近傍の動径分布関数を XAFS 測定により求めると、第一近接原子である N 原子の位置は、In 組成に強く依存せず、その最大変動量は InN 中の In-N より 2% 程度短くなる程度であり、ほぼ同じ位置を占有することが報告されている[11,14]。

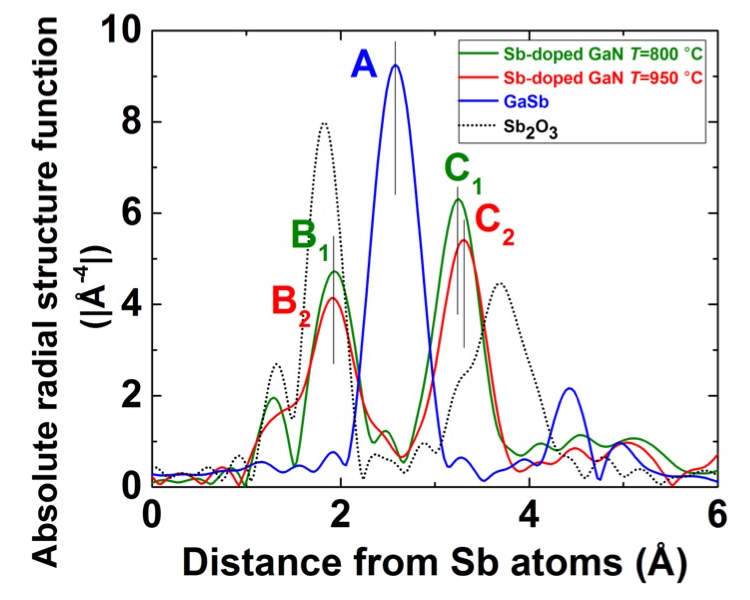
　一方で、本実験で得られた Sb 添加 GaN 中の Sb 原子近傍の動径分布関数に現れる Sb の第一近接原子と考えられる信号の位置は、GaSb で見られる Sb の第一近接原子である Ga の位置とは、一致しないばかりか、Ga の位置から －27% と ＋23～＋27% の２か所に分裂している。

　したがって、XAFS 測定の結果、本実験で用いた Sb 添加 GaN 中のほとんどの Sb は、窒化物半導体の理想的な V 族サイトを占有していないと考えられる。この試料は、Sb 添加によりX線回折で求められる平均的な格子定数が広がることから GaN_1-xSb_x 混晶半導体が形成していると考えられていたが、XAFS 測定はこのモデルを否定する結果となった。

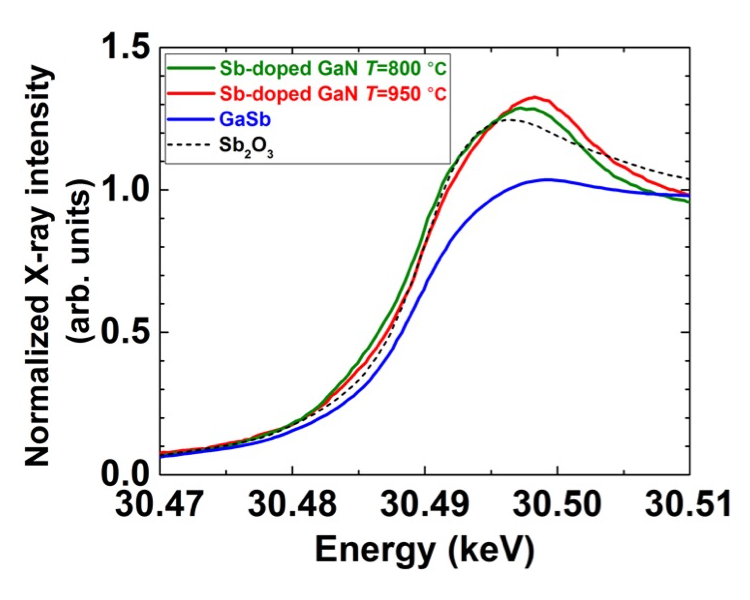
　では、添加した Sb 原子は GaN 結晶中にどのように取り込まれているのであろうか。そのモデルとして、Sb 酸化物である Sb₂O₃ の形成、または、Sb が GaN の N ではなくて Ga 原子を逆置換する２つが考えられる。前者のモデルは以下の２つの実験結果より説明可能である。１つ目は、図５に示したように、標準試料として測定した Sb₂O₃ の動径分布関数に見られる信号ピークが、Sb 添加 GaN の B1、B2 ピーク及び C1、C2 ピークの双方に比較的近い場所に現れることである。また、２つ目は、図６に示した Sb 原子の K 殻吸収端近傍の XAFS スペクトル（XANESスペクトル）を比較すると、Sb 添加 GaN の形状は、GaSb より Sb₂O₃ の形状に近いことである。更に、後者のモデルは以下のことから説明可能である。すなわち、Sb の第一近接原子である N 原子が r =2.0 Å に、第二近接原子である Ga 原子が r =3.2 Å に現れることが予測され、その位置に、Sb 添加 GaN の B1、B2 ピーク及び C1、C2 ピークが観察されることからである。ただし、Sb 添加により GaN 結晶が変形しないと仮定している。

図５．T = 800 °C 及び 950 °C で成長した Sb 添加 GaN、GaSb 基板及び Sb₂O₃ における Sb 原子近傍の位相シフト補正をした動径分布関数

図６．T= 800 °C 及び 950 °C で成長した Sb 添加 GaN、GaSb 及び Sb₂O₃ における Sb 原子の K 殻吸収端近傍の XAFS スペクトル

今後の課題：

　本報告では、X線回折スペクトルにおいて、GaN(0002)からの回折信号の低角側に観測される信号の起源として、２つのモデルを提案した。更なる考察や実験を行うことで、信号の起源を明らかにすべきと考えている。また、X線回折測定に加え XAFS 測定を行うことで、結晶成長の難しい非混和性の高い混晶半導体の成長に有益な情報を得られることから、XAFS 測定を積極的に利用して、その高品質化に貢献したい。

謝辞：

　Sb 及び Sb 酸化物を提供して下った日本精鉱株式会社に深く感謝致します。また、研究を進める上でご協力を頂いた名城大学の岩谷素顕准教授、上山智教授、赤﨑勇教授に感謝致します。

参考文献：

[1] S. Yamasaki et al., Appl. Phys. Lett. 66, 1112 (1995).

[2] K. Kumakura, T. Makimoto, and N. Kobayashi, J. App. Phys. 93, 3370 (2003).

[3] K. Kumakura, T. Makimoto, and N. Kobayashi, Appl. Phys. Lett. 79, 2588 (2003).

[4] C. G. Van de Walle and J. Neugebauer, Nature 423, 626 (2003).

[5] K. M. Yu et al., Appl. Phys. Lett. 102, 102104 (2013).

[6] S. H. Moon et al., J. Mater. Res. 24, 3569 (2009).

[7] T. Suzuki et al., The 10th International Conference on Nitride Semiconductors (ICNS), A9.07 (2013).

[8] D. Komori et al., Jpn. J. Appl. Phys. 55, 05FD01-1 (2016).

[9] R. V. Sapelkin et al., Phys. Rev. B 56, 11531 (1997).

[10] K. E. Miyano et al., Appl. Phys. Lett. 70, 2108 (1997).

[11] T. Miyajima et al., phys. stat. sol. (b) 228, 45 (2001).

[12] J. C. Mikkelsen, Jr. and J. B. Boyce, Phys. Rev. Lett. 49, 1412 (1982).

[13] T. Miyajima et al., phys. stat. sol. (b) 234, 801 (2002).

[14] N. J. Jeffs et al., Mater. Res. Soc. Symp. Proc. 512, 519 (1998).

[15] R. Seiki et al., International Workshop on Nitride Semiconductors (IWN) 2016, D1.3.06 (2016).

(Received: September 5, 2018; Accepted: December 16, 2019; Published: January 22, 2020)