Volume7 No.2

背景と研究目的：

　電磁波や粒子線を利用した顕微鏡の空間分解能は、およそ用いる電磁波や粒子線の波長と同程度である。従って波長が 0.1 nm 程度の硬X線を用いれば、原子分解能の顕微鏡が実現するはずである。しかしX線領域では、期待される空間分解能を満たす精度でレンズを加工することが不可能なため、原子分解能のX線顕微鏡は実現しない。そこでレンズの代わりに計算機を用いることでイメージングを行う試みが最近多くなされるようになった。この方法は lensless imaging と総称される。試料によるX線の散乱とは試料の電子密度分布のフーリエ変換(構造因子)であるから、これにもう一度フーリエ変換を行なうことで電子密度分布の実空間像を高い倍率で復元できるはずである。ところが構造因子は複素数で、振幅と位相の情報を持つのに対し、X線検出器は振幅しか記録できず、位相情報が失われてしまうのが問題である(位相問題)。この問題を解決するため、2つの方法が用いられる。1つは繰り返し計算により、失われた位相を徐々に回復する方法(Coherent Diffractive Imaging、CDI 法)[1]であり、1つは位相情報を回折像自体に埋め込む方法(フーリエ変換ホログラフィー法(Fourier Transform Holography、FTH 法)[2]である。CDI 法の実体はモデルフィッティングで、その成功率は回折像の S/N 比など多くの要素に左右され、データに missing pixel (ビームストップや検出器の飽和などによって正しいデータが記録されていないピクセル)などの欠陥があると計算結果が収束せず、複数回計算を行なうとその都度結果が異なったりする。それに対し、FTH 法では位相情報自体は保存されているため、一義的に構造が復元され、繰り返し計算も必要ない。その代わり FTH 法では、試料との間に干渉を起こす参照物体を適切な位置に配置する必要がある。

　本研究は、試料である生体分子と参照物体を適切な位置関係に固定する媒体として DNA 折り紙[3]を用い、FTH 法により試料のイメージングを行う試みである。DNA 折り紙とは、長い1本鎖 DNA とオリゴ DNA の間で2本鎖を形成させることで自在な 2-3 次元ナノ構造体を形成させる技術で、この折り紙の特定部位に蛋白や金ナノ粒子を結合させることも可能である。そこで、蛋白分子と金ナノ粒子の干渉を記録することで FTH 法により蛋白分子のイメージングを行うことが究極の目標である。蛋白の1分子からのX線散乱は極めて弱いため、解析可能なデータを得るためには蛋白と金ナノ粒子を結合した折り紙を同じ向きでタイル状に多数並べる必要があり、技術的なハードルは極めて高い。そこで、折り紙に複数の金ナノ粒子を配置し、金ナノ粒子同士の干渉を記録することを最初の目標として実験を行なった。

実験：

　図１が今回の実験のためにデザインされた折り紙で、径 10 nm の金ナノ粒子が複数個所に配置されている。これの懸濁液を 100 nm の厚さの窒化シリコン膜に滴下し、吸着させたうえ乾燥させたものを試料とした。X線散乱像の記録はBL40XUビームラインで行い、10+15 μm 径のピンホールでマイクロビームを作成し、Xenocs 製スキャッタレススリットでピンホール由来の寄生散乱をカットした。この種の実験では極小角領域のデータが重要であり、極小角領域の寄生散乱をできるだけカットするためスキャッタレススリットを2組直列に並べる試験も行なったが、調整に労力を要する割には効果が少なく、データは1組のスキャッタレススリットを用いた光学系で取得した。X線のエネルギーは 8 keV(λ = 0.15 nm)でサンプル-検出器間距離は約 3.5 m、検出器としてはピクセルサイズを小さくできるイメージングプレート(IP)を 50 μm のピクセルサイズで用いた。露光は30秒である。IP はデータの読み出し、消去に時間がかかるため、露光1枚ごとに読み出しを行なうのは非効率である。そこで、IP の前に 60x60 mm の開口部をもつ真鍮板を置き、XZ型に配置した自動ステージで IP を移動させ、露光を繰り返した。この方法により、20x25 cm サイズの IP 1枚につき9回の露光を可能にした。

図１．実験に使用したDNA折り紙の電子顕微鏡写真。10 nm の金ナノ粒子が5個結合している

結果および考察：

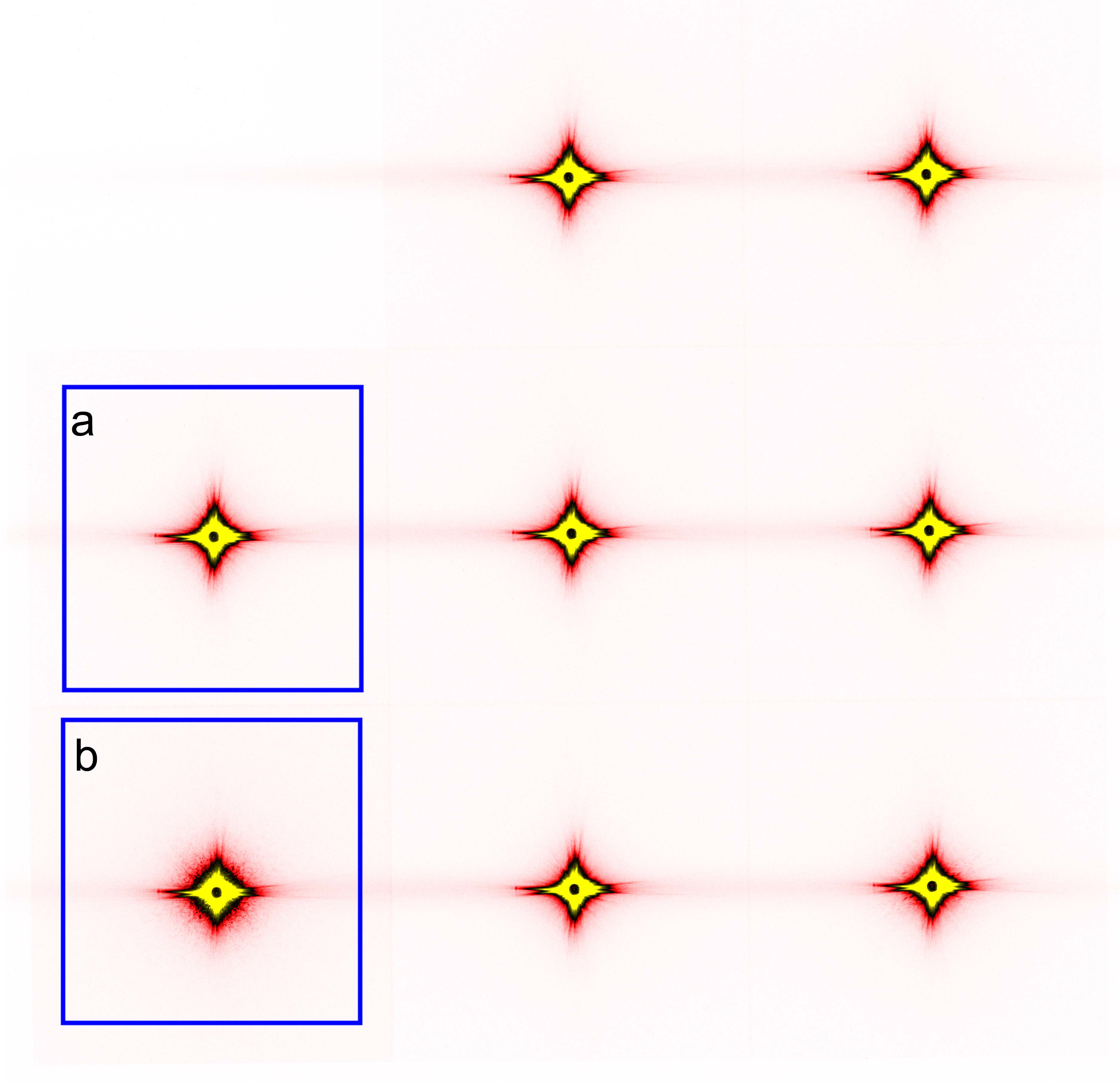
　IP 上に記録された散乱像の例を図２に示す。確率的には、径 10 μm の照射エリアには必ず DNA 折り紙が存在しているはずであるが、径 10 nm の金ナノ粒子からの散乱は極めて弱く、殆どの露光において金ナノ粒子同士の干渉に由来すると思われる散乱は認められなかった。しかし、一部の散乱像には、何らかの物体から散乱されたと思われる像が明瞭に記録されていた(図２のb)。そこで、この散乱像から、散乱物体がないと思われる像(図２のa)を差し引いて、散乱物体だけからの散乱像を求めた(図３a)。多数のスポットが記録されており、これらがフリーデル則を満たしていることから物体からの真の散乱であり、ノイズではないことが示唆された。そして、これがどんな物体に由来するのかを CDI 法により調べてみた。

図２.　1枚のIPに記録された散乱像。窒化シリコン膜の異なる位置からの散乱像が8個記録されている。

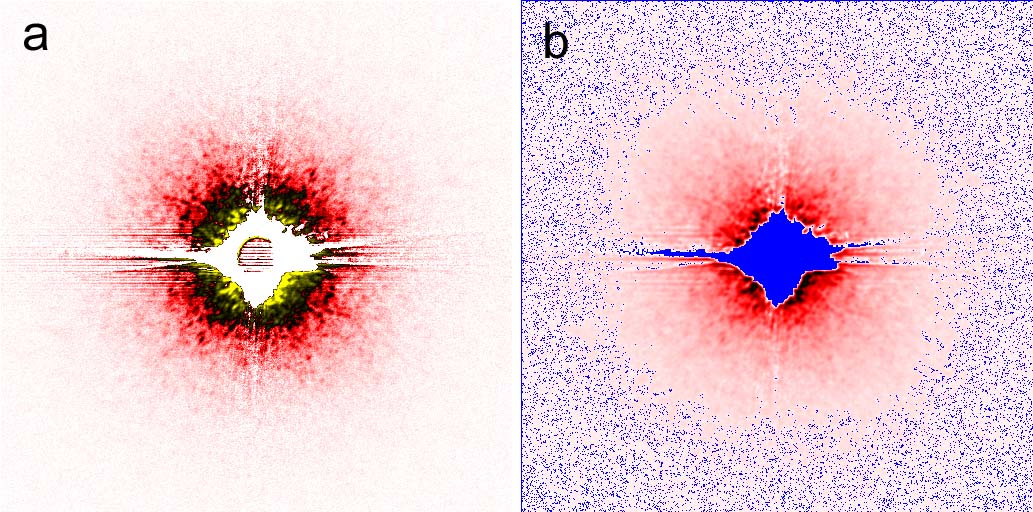
図３.　CDI計算に用いた散乱像(a)。図３のｂからａを差し引いたもの。Missing pixel 領域は(b)の青で示す。

　計算は、CDI で最も広く用いられている HIO 法(Hybrid Input-Output)[4]に、サポートのサイズを可変にする shrink-wrap 法[5]を組み合わせて用いた。散乱像のデータの平方根を求めてこれを構造因子とし、IP の飽和領域やビームストップなどの missing pixel 領域(図３bの青の領域)は計算から除外した。

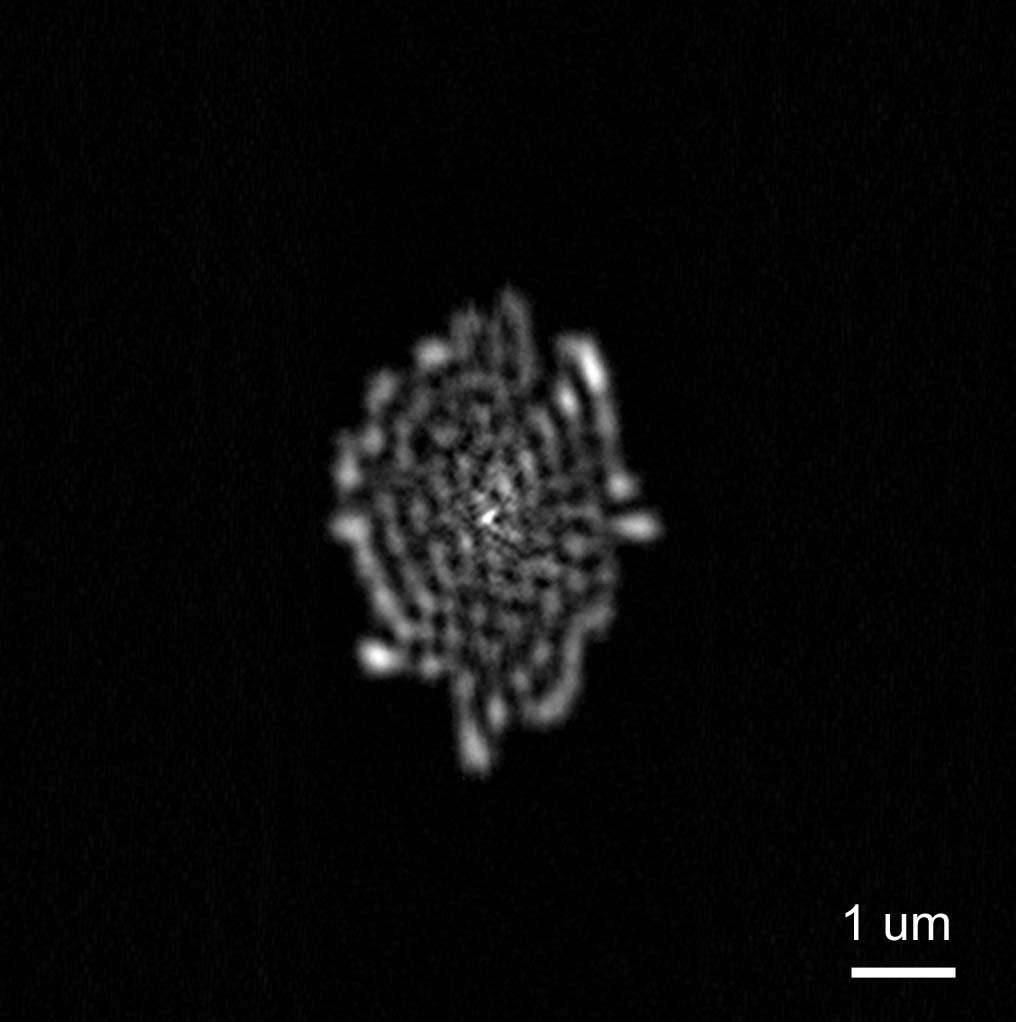
　図４が図３の散乱像から復元された散乱物体の画像である。この計算は元の散乱像(1200x1200 ピクセル)から、中心の 512x512 ピクセルを切り出して行なった。示したのは 40000 回の繰り返し計算の結果で、最終的な誤差関数(サポート外の密度/サポート内の密度。具体的な式は文献[6]参照)の値は 13.7％ であった。この値は大まかな形状としては大体正しいが、細部には誤りの可能性があることを示す。通常は誤差関数が 1% であれば、目視では正しい形状と区別がつかない程度である。

　　　　　　　　　　　　　図４.　CDI計算により復元された散乱物体の画像。

　再生されたものは約 3x4 μm の大きさの楕円形の物体であり、使用した折り紙1個のサイズより遥かに大きいため、多数の折り紙が凝集したものと予想される。

　得られた結果は当初期待していたものではないが、DNA 折り紙を使用した実験で初めて実空間イメージングが実現した意義は大きい。またBL40XUのX線のエネルギーバンド幅は 2% あるが、今回の結果はバンド幅が広くても CDI 法によるイメージングが可能であることを示している。

今後の課題：

　FTH 法の空間分解能を決めるのは参照物体のサイズになるので、計 10 nm の金ナノ粒子を用いれば 10 nm の分解能が期待できる。しかし今回の結果から 10 nm の金ナノ粒子を結合させた折り紙単独からの散乱を記録するのは困難であるのが明らかで、所期の成果を得るためには折り紙をタイル状に(2次元結晶状に)並べる技術を開発することが必須であろう。

参考文献：

[1] S. Marchesini et al. Opt. Express. 11, 2344-2353 (2003).

[2] I. McNulty et al., Science, 256, 1009-1012 (1992).

[3] P.W. Rothemund. Nature, 440, 297-302 (2006).

[4] J. R. Fienup, Appl. Opt. 21, 2758-2769 (1982).

[5] S. Marchesini et al., Phys. Rev. B, 68, 140101(R) (2003).

[6] J. Miao & D. Sayre. Acta Cryst. A, 56, 596-605 (2000).

(Received: March 14, 2019; Early edition: May 9, 2019; Accepted: July 16, 2019; Published: August 29, 2019)