Volume7 No.2
SPring-8 Section A: Scientific Research Report
液体Se50-Te50混合系の液体-液体相転移に伴う密度ゆらぎの変化:
単色X線による測定
Density Fluctuations of Liquid Se50-Te50 Mixture at Continuous Liquid-Liquid Phase Transition Observed by Monochromatic X-ray
a広島大学、b(公財)高輝度光科学研究センター
aHiroshima University, bJASRI
- Abstract
-
液体 Se-Te 混合系は温度や組成の変化により、連続的な構造転移を示すことが古くから知られている。転移に伴い密度がメゾスコピックに不均質になることが1980年代には提唱されていたが、永らくその実験的な証拠は得られていなかった。この問題に対して我々は、SPring-8/BL04B2を利用した小角X線散乱測定により、その微小な密度ゆらぎの変化を検知することに初めて成功し、2012年の論文で発表した。ただこの実験には不備な点が一つあった。BL04B2は分光結晶が一枚ふりであるため入射光への高調波の混入を避けらないが、検出器にエネルギー分解能のないイメージングプレートを使用したため、完全な単色X線の散乱スペクトル測定ではなかった。そこで今回、Ge半導体検出器とシングルチャンネルアナライザーから成る測定システムを用いることで、散乱光をエネルギー選別した測定を行い、前回の実験結果の妥当性の検証を行った。
Keywords: 液体-液体相転移、密度ゆらぎ、小角散乱
背景と研究目的:
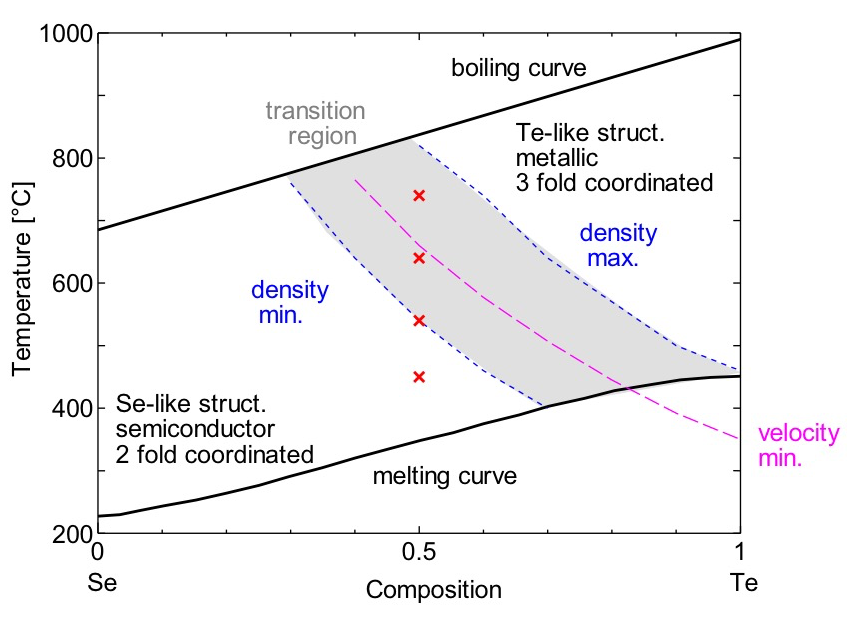
Se-Te 系は全率固溶の2成分系である。液体相にあっては、温度や組成を変化させることにより、液体 Se に類似の2配位的な低密度構造から、液体 Te に類似の3配位的な高密度構造へと連続的に転移することが調べられている[1-3]。この転移は半導体から金属への変化も伴っている。また転移領域では、温度上昇に伴う負の熱膨張係数[4]や音速の極小[5]など、顕著な熱力学異常も観測されている(図1参照)。熱力学異常を含め、本系の現象を包括的に説明するモデルとして、転移領域では両相がメゾスコピックに混ざり合っているとする「不均質モデル」が1980年代には提唱されていた[6]。ただ不均質性については当時直接的な実験証拠はなく、また「熱平衡な液体が不均質になり得ていいのか?」という本質的な問いも相まって、永らく論争になっていた。
この課題に対して、我々はSPring-8を用いた液体 Se-Te 混合系の小角X線散乱を行い、転移に伴う微小な密度ゆらぎの変化、および転移領域の中心でその強度が極大を示すことを初めて観測し、2012年に論文発表した[7]。この密度ゆらぎの変化は、組成や圧力を変えた場合も転移に連動して変化しており、密度ゆらぎの起源が連続相転移であることも立証した。
ただこの実験結果は、定性的な変化としては十分な証拠であったものの、測定した散乱光には、(分光結晶が一枚であることによる)高調波散乱や、Te の蛍光成分など正味の試料からの散乱ではない成分も含まれていた。いくつかの工夫によりこれら余分な成分を見積り、バックグランドとして取り除いてはいたが、実験の不完全性が残されていた。そこで今回、Ge 半導体検出器とシングルチャンネルアナライザーを用いた計測システムを用い、測定光をエネルギー選別して高調波成分や Te の蛍光成分を有意に除去することで、これまでの結論の検証を行った。
実験:
実験を行ったビームラインは前回[7]と同じBL04B2で、入射光はシリコンの(2 2 0)結晶面を用いて 62 keV に分光しているが、124 keV の高調波が 10% 程度以下混入していることがわかっている。測定システムについては、前回は「超臨界融体用X線小角散乱回折計」を用い、試料の後ろ 2960 mm のカメラ長の位置にイメージングプレートを配置して測定していた。今回は「非晶質物質用二軸回折計」を用い、ゴニオメーター中心に配した試料からの散乱光を、散乱角度を制御しながら Ge 半導体検出器で検知、シングルチャンネルアナライザーで測定エネルギー範囲を 55-63 keV に制限することにより、単色X線の回折測定を行った。高温の液体試料を導入する試料容器については、前回同様の自作のサファイア製[8]を用いた。試料雰囲気を制御するチャンバーについては、前回は主に高圧容器(耐圧 2000 気圧)を用いたが、今回は実験の簡便性のため常圧容器(10気圧以下)を用いており、ヘリウムガス約 1.5 気圧雰囲気下での測定とした。表1にこれら測定条件をまとめた。また図1には測定試料の温度条件を液体 Se-Te 混合系の相図上に示す。測定については試料の他、別途試料容器のみの測定も行っており、これを差し引くことで、試料からの散乱のみの情報を抽出している。
| 前回(2012年論文) | 今回 | |
| ビームライン 入射X線 |
BL04B2 62 keV+124 keV(5-10%) |
|
| 検出システム | イメージングプレート (エネルギー選別能無し) |
Ge半導体検出器 +シングルチャンネルアナライザー (エネルギー選別可能) |
| カメラ長 | 2960 mm | 950 mm |
| 有効 Q 範囲 [nm-1] | 0.8 – 10 「小角X線散乱」 |
1.4 – 80 「X線回折」 |
| 試料容器 | 自作サファイア製容器 | |
| チャンバー | 高圧容器/常圧容器 | 常圧容器 |
図1.液体Se-Te混合系の組成-温度相図と今回の測定条件(×印)
結果および考察:
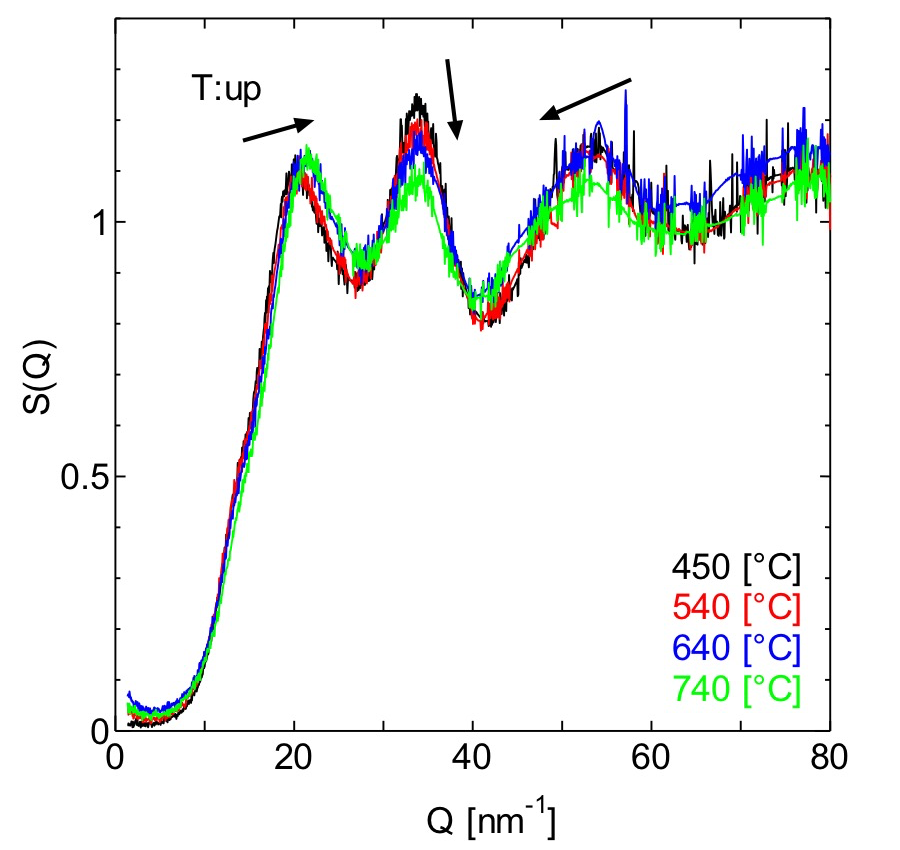
測定された試料散乱の強度は、試料の透過率と密度、各元素の原子形状因子を考慮し、Krogh-Moe-Norman 法を用いた標準的な方法[9]で規格化を行い、構造因子 S(Q) を導出した。なお試料密度については、今回は直接測定を行っていないので、温度に対応した文献値[4]を用いている。導出した S(Q) を図2に示す。第1、第2、第3ピークがそれぞれ Q =20、34、53[nm-1]付近に見えており、過去のX線[1]や中性子[2,3]の測定結果と矛盾はない。また温度上昇に伴い、第1ピークは高 Q 側へシフト、第2ピークは強度が減少、第3ピークは低 Q 側にシフトしているが、これも過去の中性子散乱の結果[3]と定性的に一致している。温度上昇にもかかわらず第一ピークの位置が高 Q 側にシフト=第一近接原子間距離が収縮していることは、マクロな密度測定で負の熱膨張を示していることと矛盾はなく、低密度相から高密度相へ構造相転移が起こっていることが確認される。またこれら広波数側の温度変化は温度に対して単調変化であることも留意するべき点である。局所構造の変化は相転移の中心(約 650℃、音速の極小領域)をまたいでも単調である。
図2. 構造因子 S(Q)
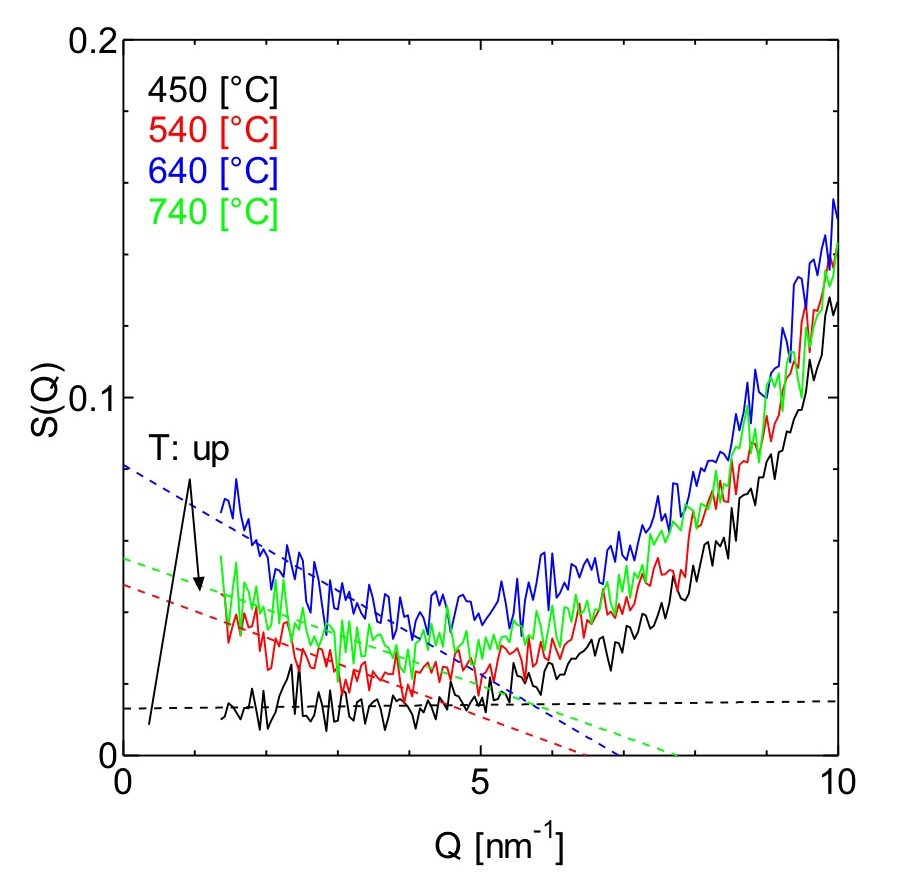
図3. 構造因子 S(Q) の小角領域
一方図3は、図2の低波数部分を拡大したものである。注目すべき点は Q が 4[nm-1]以下の領域である。低温領域(450 → 640℃)では温度上昇に伴い、散乱強度は大きく、Q に対する傾きは大きくなっていく。しかしながらより高温側(640 → 740℃)では強度、傾き共に小さくなる。つまり相転移中心付近で密度ゆらぎが極大を示しており、前回論文の主要な結論がこれで検証された。また 4[nm-1]付近を境として高波数域(図2)と低波数域(図3)が別の温度変化を示すという今回の結果を我々は以下のように考えている。高波数域が対応する局所構造は、原子間の結合の影響を強く受けている。結合は低温下に伴いより強くなり、結果としてより大きな構造としての「中距離構造」は成長していく。一方で、低波数域が表すメゾスコピックな「ゆらぎ」は、圧縮率=マクロな熱力学の要請によって特徴付けられるものであり、相転移領域で極大を示す。低温下に伴い一時は成長するが、更なる温度低下では減少することが予想される。実際に今回の高波数/低波数の結果は、これらの2つの似ていて非なる起源の現象が液体には存在し、それが反映されたことを示唆している。近年、高波数域の精密測定の実験データに対して逆モンテカルロ法など詳細な解析を行うことで、局所構造を超えた3次元の「中距離構造」をモデリングする技術が進歩している。しかし低波数域の実測データの欠落は、「ゆらぎ」の影響を考慮できずに重大な過ちを導く可能性を示しており、その重要性を主張したい。
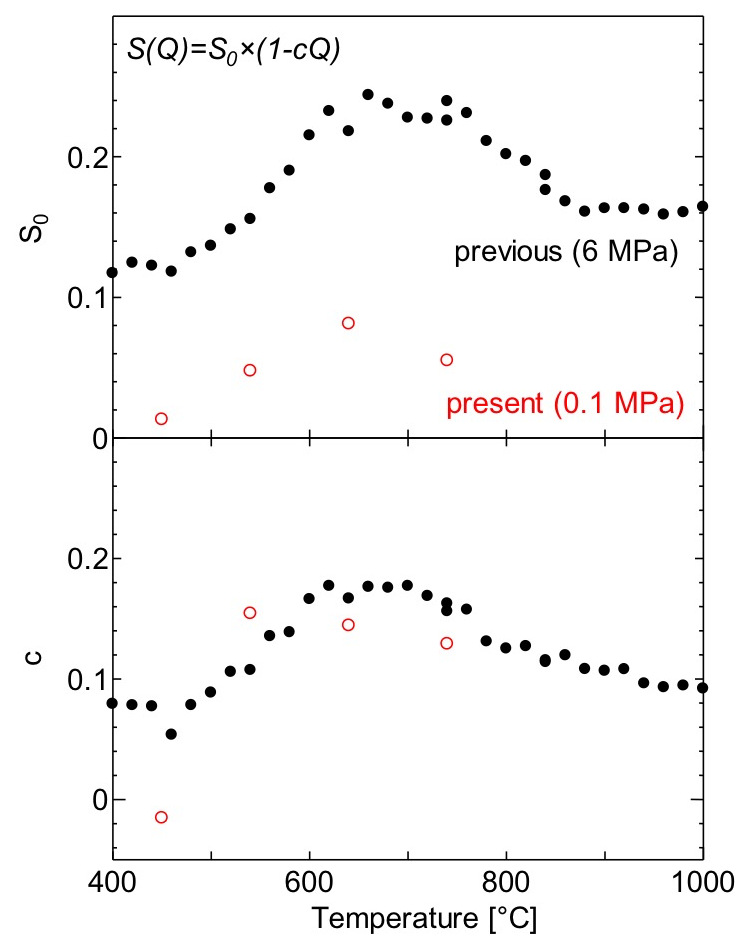
最後に、図3の低波数域(Q <4 [nm-1])の S(Q)を直線近似、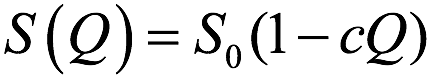 した際のパラメータを図4に赤印で示す。前回の結果も同じ図に黒印で示す。フィットで得られたパラメータのうち S0 は、構造因子 S(Q) の Q → 0 極限で、マクロな熱力学量である圧縮率 κT と
した際のパラメータを図4に赤印で示す。前回の結果も同じ図に黒印で示す。フィットで得られたパラメータのうち S0 は、構造因子 S(Q) の Q → 0 極限で、マクロな熱力学量である圧縮率 κT と 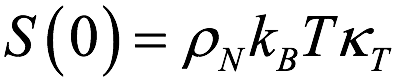 (ρN: 数密度、kB:ボルツマン定数、T :温度)の関係にあり、密度ゆらぎの大きさに対応する。同様に c は密度ゆらぎのメゾスコピックな空間サイズを示す値である。c については、前回と今回でほぼ矛盾しない結果が得られている。一方 S0 については前回と今回で、640℃ 付近で極大を示すという温度変化は定性的に一致しているが、その絶対値は大きく異なっている。この相違は、前回と今回の若干の測定条件の差(試料圧力、利用したデータの Q 範囲)によるものではなく、有意な不一致であると認識している。この原因については残念ながら現時点では明らかにできていない。前回の測定では、高調波や蛍光成分あるいは高圧の He ガス雰囲気からの散乱の見積もり、が不完全であった可能性があるが、同様の手続きで求めた Te の S0 は圧縮率(密度の圧力依存性[10])から見積もった値とほぼ一致していた。一方今回の測定では高調波や蛍光成分は測定段階で除去できているが、解析にやや不完全なところがある。今回採用した Krogh-Moe-Norman 法は、散乱強度の小さい高波数域の S(Q) を物理的に矛盾無いもの(1の近傍で振動する)に補正する効果はあるが、低波数域の絶対値が正しい値になることは必ずしも保証されていないからである。絶対値としてどちらが正しいのかは、圧縮率から求められる S0 と比較するのが良いが、残念ながら混合系については精度の高いデータが存在しないため現時点では判断できない。散乱測定による S0 の絶対値の決定方法については、今後の課題として残ることとなった。
(ρN: 数密度、kB:ボルツマン定数、T :温度)の関係にあり、密度ゆらぎの大きさに対応する。同様に c は密度ゆらぎのメゾスコピックな空間サイズを示す値である。c については、前回と今回でほぼ矛盾しない結果が得られている。一方 S0 については前回と今回で、640℃ 付近で極大を示すという温度変化は定性的に一致しているが、その絶対値は大きく異なっている。この相違は、前回と今回の若干の測定条件の差(試料圧力、利用したデータの Q 範囲)によるものではなく、有意な不一致であると認識している。この原因については残念ながら現時点では明らかにできていない。前回の測定では、高調波や蛍光成分あるいは高圧の He ガス雰囲気からの散乱の見積もり、が不完全であった可能性があるが、同様の手続きで求めた Te の S0 は圧縮率(密度の圧力依存性[10])から見積もった値とほぼ一致していた。一方今回の測定では高調波や蛍光成分は測定段階で除去できているが、解析にやや不完全なところがある。今回採用した Krogh-Moe-Norman 法は、散乱強度の小さい高波数域の S(Q) を物理的に矛盾無いもの(1の近傍で振動する)に補正する効果はあるが、低波数域の絶対値が正しい値になることは必ずしも保証されていないからである。絶対値としてどちらが正しいのかは、圧縮率から求められる S0 と比較するのが良いが、残念ながら混合系については精度の高いデータが存在しないため現時点では判断できない。散乱測定による S0 の絶対値の決定方法については、今後の課題として残ることとなった。
図4. 密度ゆらぎのパラメータ
まとめ:
連続相転移を行う液体 Se50-Te50 混合系に対して、62 keV の単色X線を用いたX線回折測定を行い、構造因子 S(Q) を導出した。低波数領域(Q <4[nm-1])の S(Q) の温度変化から、密度ゆらぎが転移領域の中心付近で極大を示すことが結論づけられた。これにより前回2012年の論文の主たる結論が検証できた。また高波数域の温度変化は、今回の温度範囲(450 から 740℃)で単調に構造が収縮していることを示しており、低密度相から高密度相への相転移が起こっていることが検証できた。これら低波数域と高波数域の S(Q) の温度変化は約 4[nm-1]付近を境に異なる振る舞いを示しており、高波数に対応した「局所」構造と低波数に対応した「中距離」構造(=メゾスコピックなゆらぎ)は基本的に別物であることを示している。低波数域に対応する小角散乱測定の重要性が示唆される。
参考文献:
[1] W. Hoyer, E. Thomas, and M. Wobst, Z. Naturforsch., 30a, 1633 (1975).
[2] R. Bellissent and G. Tourand, J. Non-Cryst. Solids, 35-36, 1221 (1980).
[3] A. Chiba et al., J. Phys. Soc. Jpn., 71, 504 (2002).
[4] Y. Tsuchiya, J. Phys. Soc. Jpn., 57, 3851 (1988).
[5] Y. Tsuchiya, J. Phys. Soc. Jpn., 60, 960 (1991).
[6] Y. Tsuchiya and E. F. W. Seymour, J. Phys. C: Sol. Stat. Phys., 15, L687 (1982).
[7] Y. Kajihara et al., Phys. Rev. B, 86, 214202 (2012).
[8] K.Tamura and M. Inui, J. Phys.: Condens. Matter, 13, R337 (2001).
[9] 早稲田嘉夫、松原英一郎、「X線構造解析」(内田老鶴圃) (1998) 第12章.
[10] R. Barrue and J. C. Perron, Phil. Mag. B, 51, 317 (1985).
(Received: February 22, 2019; Early edition: April 10, 2019; Accepted: July 16, 2019; Published: August 29, 2019)