Volume7 No.1

Background and Purpose

The existence of incipient electronic orders distinct from and competing with superconductivity is one of the salient features of high-Tc superconductors. Increasing evidence suggests that a generic type of primary competing orders in the superconducting regime is charge density wave, which takes different forms in different cuprate families [1]. The relationships between these various forms of the competing charge orders, their exact natures and origins are currently central open questions of the field. The answers to these questions would constitute a key step towards the resolution of the high-Tc mystery.

Recent experimental developments have pointed to a common, broken chiral (aka, parity) symmetry nature of these charge orders. The most notable evidence came from the observation of a (polar) Kerr rotation onset at the charge ordering temperature in La_2-xBa_xCuO₄ with hole doping level x=1/8 (LBCO-1/8) [2]. Kerr rotation can in principle arise from ferromagnetic or chiral materials. In the case of LBCO-1/8, nevertheless, (antiferro-)magnetic order is known to set in at a lower temperature than the Kerr rotation onset. Onsets of the Kerr rotation have also been observed in other cuprate families, such as Y-based [3], Bi-based [4] and Hg-based [5], at some characteristic temperatures, TK, again well above the magnetic ordering temperatures (if not zero). X-ray scattering on Y-based [6] and, most recently, on Bi-based [7] further support the picture that the charge orders, despite their much reduced correlation lengths, set in around TK and, therefore, share the same essential character with the charge order in LBCO-1/8, which is likely chiral rather than magnetic.

LBCO-1/8 and Kerr effect both hold unique positions in the related studies. That the Kerr onset in LBCO-1/8 appears to be more abrupt and the maximal size of Kerr rotation is ~5 times larger than seen in other cuprates plausibly hints at a remarkable strength of the chirality tied to the robust charge order in this system. However, some key ambiguities remain as to the microscopic origin of the Kerr effect and its alternative interpretations based on some exotic forms of magnetism (intrinsic or extrinsic) hypothesized to exist in the system [8]. An independent experimental study with an element-specific probe for the CuO₂ electronic states of LBCO-1/8 preferably on a different physical quantity that relates to chirality and magnetism in a different way, is expected to yield important and complementary insights about the possible chiral symmetry breaking and to provide a needed anchor for future studies of other cuprate families. X-ray natural circular dichroism (XNCD) is such a physical quantity of interest that has been proposed to provide unique fingerprint information about the chiral charge orders in cuprates [9].

Experimental Summary

In order to unveil the chiral nature of the charge order and to settle important open questions left behind by the Kerr effect study on the same material, we have performed a temperature- and angle-dependent x-ray circular dichroism (XCD) study on the high-temperature cuprate superconductor LBCO-1/8 near the Cu K-edge at the BL39XU beamtime of SPring-8 and ID12 of ESRF. Circular dichroism in absorption/transmission is an important manifestation of optical activity of materials, which generally has a magnetic (XMCD) and/or non-magnetic (XNCD) origin. For non-magnetic materials, circular dichroism is dominated by the pseudoscalar part of the optical activity tensor at optical wavelengths—relevant to the Kerr effect—but in the x-ray range (i.e., XNCD) by the pseudo-deviator part [10]. In our experiments, we paid attention and spent effort to eliminating/minimizing the elastic scattering artifacts and linear dichroism (XNLD) contamination of the measured signal. As a result, we succeeded in observing a XCD signal that showed an abrupt onset in the charge-ordered state of LBCO-1/8. Based on these preliminary results, we were able to present strong arguments for the non-magnetic nature of this signal and found a reasonable agreement with the existing theoretical calculation for the possible XNCD in a related cuprate material. This finding, if confirmed by future experiments, will shed important new light on a central open question of the high-Tc field—the nature and microscopic origin of the charge order as one of the primary competing orders for superconductivity, and constitute the first unambiguous x-ray evidence for the electronic (as opposed to the structural) chirality in a condensed matter system.

Results and Discussion

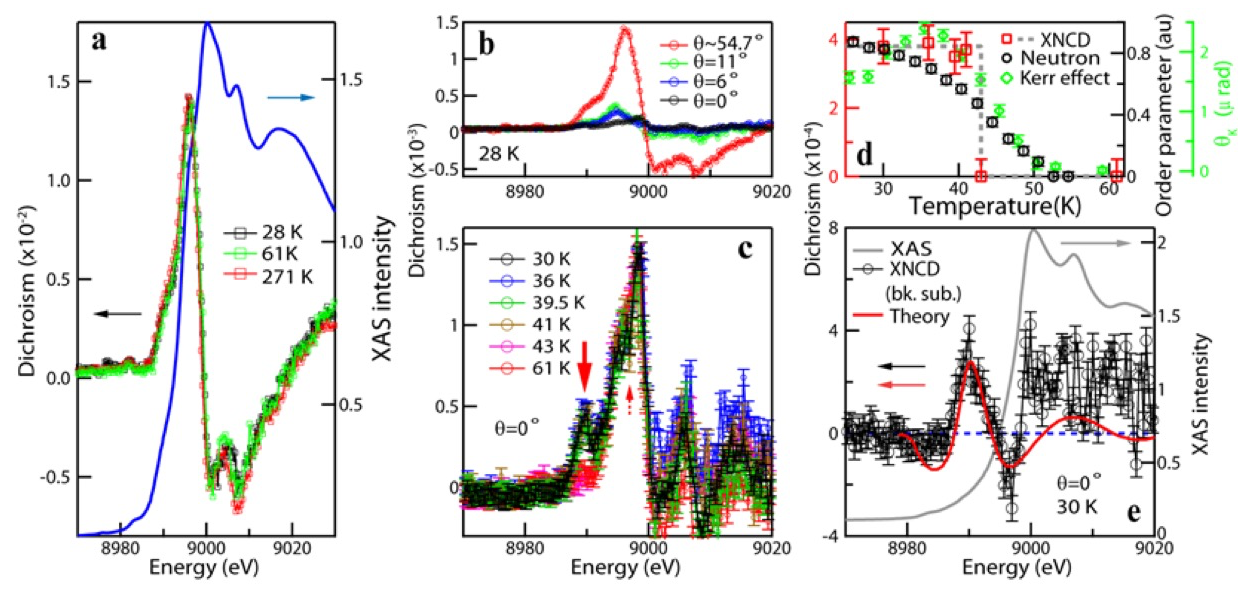
We calculated the dichroic spectrum based on the difference in x-ray absorption spectra measured, respectively, with left and right circularly polarized x-ray incidences. We first noted a dichroic signal which is largely temperature independent (Fig. 1a; see figures attached at the end) and whose overall magnitude increases with the increase of the incidence angle of light away from normal incidence (Fig. 1b). We ascribed this signal to the x-ray natural linear dichroism (XNLD), which reflects the crystallographic asymmetry between the a-axis and the c-axis that was probed upon switching the residual linear polarization components of the incident light with ~90% circular polarization. Interestingly, near the normal incidence where XNLD is small, we observed an additional dichroic signal emerging on top of the XNLD signal upon decreasing temperature (Fig. 1c). Its strength showed an abrupt onset across ~42 K (Fig. 1d). After removal of the XNLD background, this low-temperature signal features a distinct peak at ~8.99 keV and a few sign changes right below the edge (Fig. 1e).

Fig. 1 X-ray absorption (XAS) and dichroic spectra at (a) selected temperatures and (b) θ, which denotes the angle between the x-ray wavevector and the c-axis of the crystal. (c) Dichroic spectra at low temperatures and θ=0˚ (normal incidence), showing the appearance of additional features. (d) Temperature dependence of the intensity of the dichroic feature marked by the big red arrow in (c), compared with those of the square root of the spin ordering neutron diffraction peak intensity [13] (reflecting the magnetic moment size) and the Kerr rotation [2] measured on LBCO-1/8. (e) XAS and background-subtracted dichroic spectrum at θ=0˚, compared with the calculated XNCD spectrum. Note the common y-scale for the calculated and experimental dichroism.

As LBCO-1/8 is in the low-temperature tetragonal (LTT) structural phase below 54 K which is uniaxial, no XNLD signal is expected from any ab-plane crystallographic asymmetry, although one would need to study the sample azimuthal rotation angle φ (about the c-axis) dependence of the low-temperature signal to firmly exclude its XNLD nature; for which XNLD varies as cos2φ while XCD should be φ independent [11]. Alternative, the signal strength of a XCD signal should follow the magnitude of the circular polarization of the incident light that one can adjust.

Thus, the observed signal is likely due to XCD, whether magnetic (XMCD) or natural (XNCD). Indeed, a spin stripe order develops around 42 K. Canted magnetic moments in an antiferromagnetic order can in principle give rise to weak ferromagnetism that can manifest in XMCD. Nevertheless, this type of XMCD signal appears unlikely to be relevant here. First, magnetic moments on Cu predominantly involve 3d electronic states. Their XMCD signal should peak at ~8.983 keV corresponding to the (dipole-forbidden) 1s-3d transition, different from the experiment. Second, unlike in a homogeneous antiferromagnetic order in the LTT phase, spin canting in the spin stripe ordered phase (<42 K) produces zero net canted moment on each CuO2 plane at low field [12]. Third, with the spin canting angle set by the Dzyaloshinsky–Moriya superexchange interaction that arises from the CuO6 octahedral tilting which saturates below 54 K, the temperature dependence of the weak ferromagnetism should follow that of the order parameter of the spin stripe order. The latter has been measured by neutron diffraction on the same material [13] (Fig. 1d), which shows a much more gradual onset behaviour than our observed XCD signal strength. XMCD can also be caused by some other non-trivial forms of broken time-reversal symmetry, e.g., in the orbital current loop order [14], nevertheless, the ordering temperatures reported so far are at least many times higher than 42 K [15] and the onsets found are anything but abrupt.

Therefore, what we newly observed below 42 K is very likely a XNCD signal. That being said, independent experimental differentiation between the XMCD and XNCD nature of the observed signal would be very helpful, which can be achieved by means of a polar angle θ dependence study; in which XNCD varies as 3cos²θ−1 while XMCD as cosθ [10]. Attempts were made to study the θ dependence at 29 K in experiment (results not shown), but because of the increasing strength of XNLD background signal with θ, the result obtained was ambiguous and incomplete. A better approach is to perform for each θ measurements at two temperatures, e.g., 35 K and 45 K (with and w/o the XCD signal), and then subtract off the XNLD background to obtain the XNCD spectrum (as shown in Fig. 1e).

To the extent that the observed signal is XNCD, its onset at 42 K coincides with the crossover of the charge stripe order from 2D (above) to 3D (below), which was observed by x-ray diffraction measured with photon energies near the Cu K-edge of similar probing depth [16]. A good correlation of the charge order along the c-axis ensures the principle axes of the local chiral orders to be aligned (with the c-axis), which is a prerequisite for the detection of a non-zero XNCD signal (because XNCD probes chirality through the pseudo-deviator part of the optical activity tensor). Kerr effect which probes the pseudo-scalar part does not require such alignment, and can in principle be sensitive to the nascent chiral order which sets in at ~50 K when it is still poorly correlated along the c-axis. Though plausible, this scenario may or may not be sufficient to explain the apparent abruptness of the XNCD onset we observed, whose implication requires further thinking.

We also compared the potential XNCD spectrum (black circles in Fig. 1e) with the theoretical calculation [9] done for a related but different cuprate material (whose crystal structural is also achiral) based on different configurations of the chiral order. We found a reasonable agreement with the results for a particular configuration (red dashed curve in Fig. 1e), in terms of the spectral line shape, positions of features and their absolute magnitudes. We are currently working on a similar theoretical calculation for LBCO-1/8 in order to determine the actual configuration of the chiral order.

Reference

[1] E. Fradkin, S. A. Kivelson, Nature Phys. 8, 864 (2012); D. K. Morr, Science 343, 382 (2014).

[2] H. Karapetyan et al., Phys. Rev. Lett. 109, 147001 (2012); H. Karapetyan et al., Phys. Rev. Lett. 112, 047003 (2014).

[3] J. Xia et al., Phys. Rev. Lett. 100, 127002 (2008).

[4] R.-H. He et al., Science 331, 1579 (2011).

[5] W. Tabis et al., arXiv:1404.7658 (2014).

[6] J. Chang et al., Nature Phys. 8, 871 (2012); G. Ghiringhelli et al., Science 337, 821 (2012).

[7] R. Comin et al., Science 343, 390 (2014); E. H. da Silva Neto et al., Science 343, 393 (2014).

[8] J. Orenstein, Phys. Rev. Lett. 107, 067002 (2011); V. Aji et al., arXiv:1211.1391v4 (2013); S. S. Pershoguba et al., Phys. Rev. Lett. 111, 047005 (2013).

[9] M. R. Norman, Phys. Rev. B 87, 180506(R) (2013).

[10] J. Goulon, A. Rogalev, C. Brouder, Comprehensive Chiroptical Spectroscopy: Instrumentation, Methodologies, and Theoretical Simulations, John Wiley & Sons, Inc. Vol. 1 (2012); J. Goulon et al., J. Synchrotron Rad. 7, 182 (2000).

[11] S. Di Matteo, M. R. Norman, Phys. Rev. B 76, 014510 (2007).

[12] M. Hücker, Phys. Rev. B 79, 104523 (2009).

[13] M. Hücker et al., Phys. Rev. B 83, 104506 (2011).

[14] V. Aji et al., arXiv:1211.1391 (2013); S. S. Pershoguba et al., Phys. Rev. Lett. 111, 047005 (2013).

[15] V. Baledent et al., Phys. Rev. Lett. 105, 027004 (2010); Y. Sidis, P. Bourges, J. Phys. Conf. Ser. 449, 012012 (2013).

[16] Y.-J. Kim et al., Phys. Rev. B 77, 064520 (2008).

ⒸJASRI

(Received: September 30, 2018; Accepted: December 17, 2018; Published: January 25, 2019 )