Volume7 No.1

Background and Purpose

Topological insulators (TIs) have attracted much attention in recent years due to their peculiar surface states which are spin-polarized and having a Dirac cone in the bulk band gap [1]. The surface states are the consequence of the bulk band inversion due to the strong spin-orbit interaction. The exceptional properties of the surface states make them be promising materials for future devices [2]. Recently ferromagnetic order was found in Mn doped TI Bi_2-xMn_xTe₃[3]. Since then intense researches have been performed both theoretically and experimentally [4-9]. Although Mn dopants at the substitutional position of Bi should act as acceptors, numbers of experimental researches show electron-like conductivity [10]. The formation of ferromagnetic order in TIs is of interest for building topological insulator-based spintronics devices [11]. However, the mechanism of the magnetic long-range order as well as detailed electronic structure of the Mn doped TI are still unclear. Since TIs are characterized by their surface states, most experimental researches on TIs were dedicated to the measurements of the surface electronic structures. The properties of the materials are, however, determined by the bulk electronic structures. In this sense bulk sensitive HAXPES is an ideal tool to investigate electronic structures of Mn doped TIs. Comparison of valence band HAXPES in pure Bi2Te3 and magnetically doped (BiMn)₂Te₃ will reveal what are the relevant states modified by the magnetic dopants and where is located the Mn contribution.

Experimental Summary

HAXPES experiments were performed for single crystals Bi_2-xMn_xTe₃ at BL15XU. We have prepared 4 samples with x = 0.10, 0.07, 0.04, and 0 in order to observe systematic changes of spectral features as a function of Mn concentration. High resolution HAXPES spectra were measured with hν = 6 keV at room temperature for Bi and Te core levels, and valence bands. Normal emission set up (take off angle 88°) was chosen in order to maximize the bulk sensitivity. The total resolution was set to be 150 meV. The Fermi energy (E_F) and the binding energy (E_B) of the spectra were calibrated by the valence band spectra for a Au reference sample.

Results and Discussion

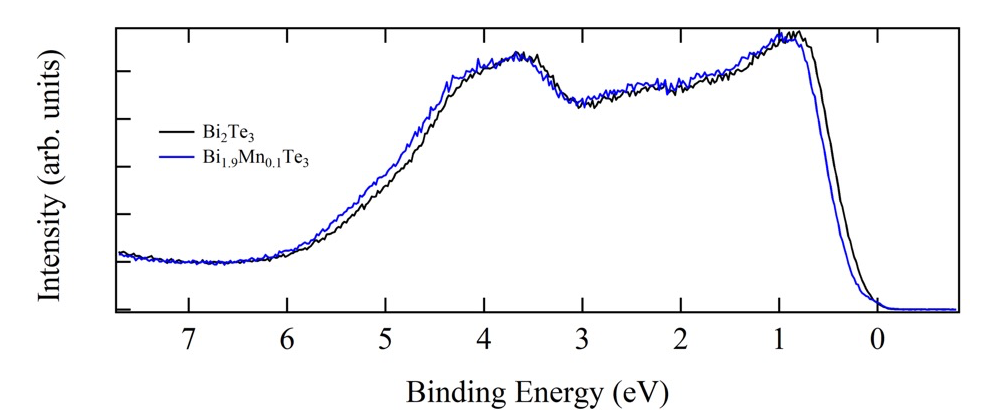
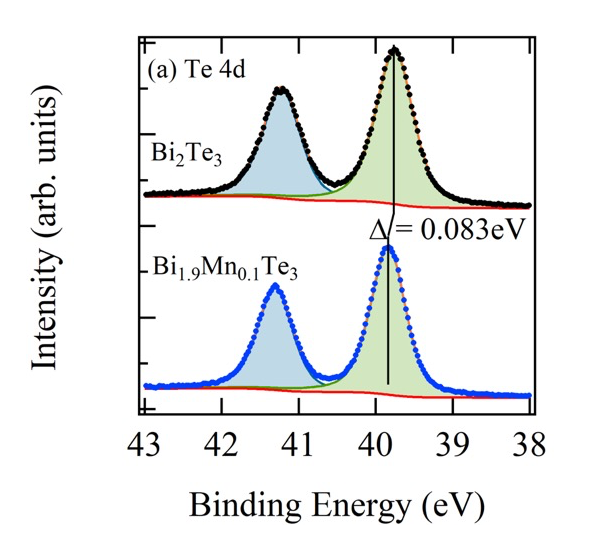
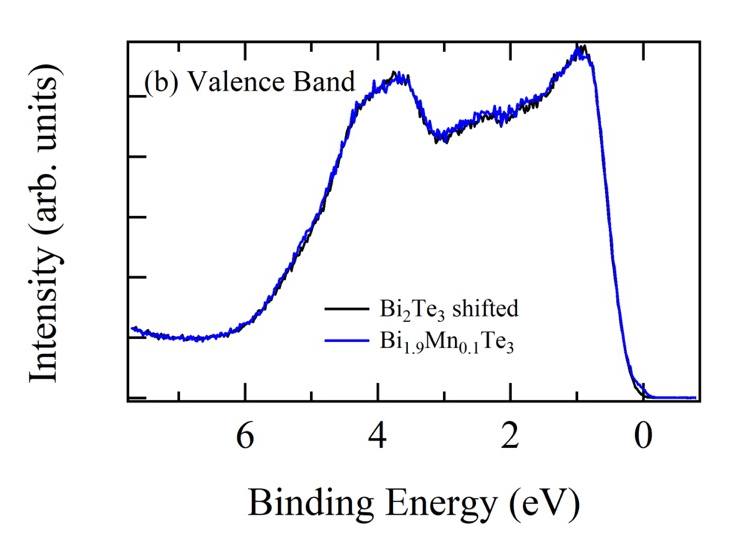
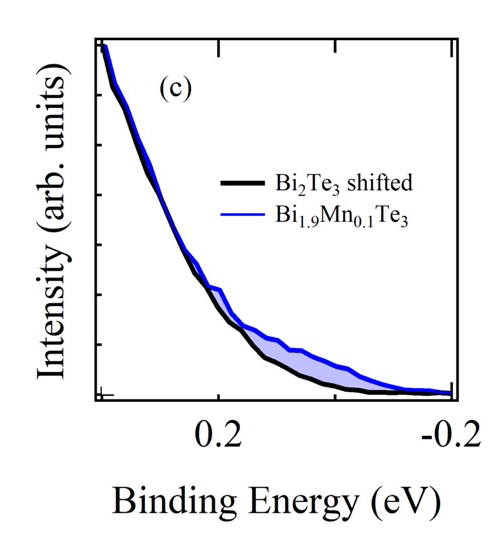
Figure 1 shows the comparison of the valence band HAXPES spectra for Bi₂Te₃ (black) and Bi_1.9Mn_0.1Te₃ (blue). The clear shift in energy of the Bi_1.9Mn_0.1Te₃ valence band spectrum is observed toward higher binding energy side compared to Bi₂Te₃ valence band spectrum by approximately 80 meV. This shift is considered due to the occupation of the states created in the band gap above the top of the valence band of Bi₂Te₃ by Mn doping. Then E_F of Bi_1.9Mn_0.1Te₃ is pinned on the Mn induced states. This is seen better when we shift the Bi₂Te₃ valence band spectrum (Figs.2 (b) and (c)). The amount of shift was determined by the energy shift of Te 4d core levels of Bi₂Te₃ and Bi_1.9Mn_0.1Te₃. The energy shift of Te 4d was obtained by the fitting with Voigt function and Shirley step function shown in Fig.2 (a). The intensity was normalized so as to minimize the sum of the square of the difference between two spectra for the binding energy range between 6.0 and 7.5 eV. Zoom up of the spectra close to E_F is shown in Fig.2 (c). The light blue shaded area shows the contribution from the Mn induced state on the Bi_1.9Mn_0.1Te₃ HAXPES spectrum.

Fig. 1. Valence band HAXPES spectra for Bi₂Te₃ (black) and Bi_1.9Mn_0.1Te₃ (blue). The clear shift in energy of the Bi_1.9Mn_0.1Te₃ valence band spectrum is observed.

Fig. 2. (a) The shift of the Te 4d peaks obtained by the fitting. The black (Bi₂Te₃) and blue (Bi_1.9Mn_0.1Te₃) dots denote the measured spectra. (b) Comparison of two valence band HAXPES spectra after the shift of Bi₂Te₃ valence band spectrum. (c) Zoom up around EF. The increase of the intensity at EF due to the Mn doping is clearly observed.

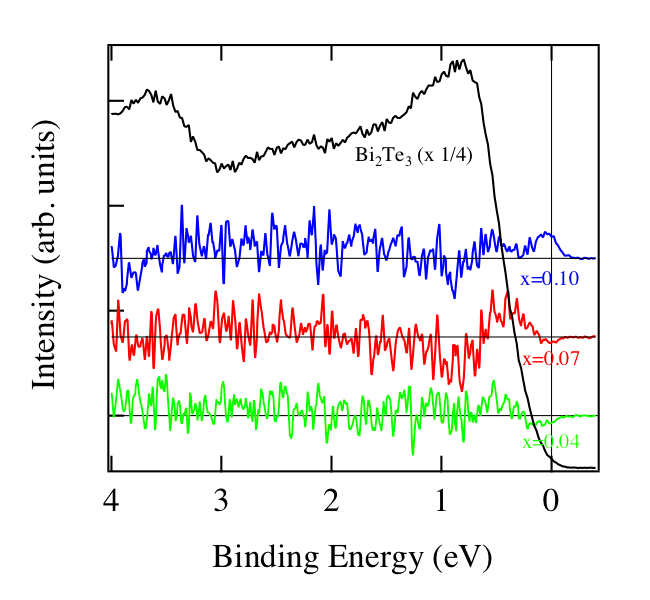
Bulk Bi₂Te₃ is a semiconductor with the band gap of 150 meV [12]. As observed in low energy angle-resolved PES spectra, surface band bending is commonly induced on Bi₂Te₃ by defects at the surface. Mn dopants modify the number of electrons in the surface states, which modifies the surface band bending, resulting in the energy shift of bulk band structure in the photoemission spectra [4]. It should be noted, however, that the carrier density of Bi_1.9Mn_0.1Te₃ is quite high (> 7 x 10¹⁹ cm^-3) and the band bending region is less than 10 nm from the surface. On the other hand the probing depth of HAXPES for nearly 6keV kinetic energy is about 20 nm, which is much larger than the surface band bending region. And the surface state contribution to the spectra is quite small. These mean that even though the band bending remains at the surface of Bi_1.9Mn_0.1Te₃, the measured spectrum reflects well the real “bulk” band structure. Suppose that the doped Mn atoms simply add electrons to the bulk system, which results in the filling of the conduction band of Bi₂Te₃. The Fermi level will be in the conduction band of Bi2Te3, which is 150 meV above the valence band top. Eventually it should make a larger shift of the band than what is actually observed by the measurements. In order to clarify the modification of the valence band by Mn doping, we made the subtraction of the Bi₂Te₃ valence band spectra from Bi_2-xMn_xTe₃ which are shifted in energy with the same manner as Fig.2. The shift for Bi_1.96Mn_0.04Te₃ and Bi_1.93Mn_0.07Te₃ are 0.004 and 0.013 eV, respectively. The difference spectrum for x =0.04 (green), 0.07 (red) and 0.10 (blue) are shown in Fig.3 with the Bi₂Te₃ valence band spectrum (black), which is multiplied by 1/4. From the blue spectrum of Fig. 3, one can clearly observe the Mn doped related peak at E_F. The spectra for the doping of x = 0.04 and 0.07 do not show such a peak but the decrease of the intensity at E_F. The absence of the Mn induced peak at E_F for x = 0.04 and 0.07 can be attributed to their relatively low carrier densities. They are 3.5 x 10¹⁸ and 5 x 10¹⁸ cm^-3 for x = 0.04 and 0.07, respectively, which are more than one order of magnitude smaller than that of x = 0.10. In fact the shifts of spectra for x = 0.04 and 0.07 are much smaller than that for x = 0.10. Except for this all of three spectra have the same tendency between E_B = 1 eV and E_F. Another Mn doping effect is observed between E_B = 1.5 and EB = 3 eV. It is the contribution of Mn 3d states according to calculations [5,9]. Since the top of the valence band of Bi₂Te₃ (the peaks at EB = 1 eV) is mainly the contribution from Te 5p states [9], the observed features of the difference spectra imply the modification of the Te 5p density of states by Mn doping.

Fig.3. Summary of the difference spectra for three doping concentration. Note that the difference spectra are offset for clarity. Black horizontal lines are the zero lines for each difference spectrum.

Challenges

We measured also angle-resolved HAXPES spectra for the TIs with hν = 3 keV at low temperature (T = 25 K) in the proposed beamtime. We did not, however, observe any band dispersion in the spectra, which can be attributed to the rather low Debye temperature (Bi₂Te₃, 165 K) of the system [13]. Recently developed soft x-ray angle-resolved PES experiments may be an alternative tool for revealing the momentum-resolved density of states of the bulk region in this system [14].

References

[1] M. Z. Hasan, C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).

[2] X.-L. Qi and S.-C. Zhang, Phys. Today 63, 33 (2010).

[3] Y. S. Hor et al., Phys. Rev. B 81, 195203 (2010).

[4] I. Vobornik et al., J. Phys. Chem. C 118, 12333 (2014).

[5] C. W. Niu et al., Appl. Phys. Lett. 98, 252502 (2011).

[6] A. Ghasemi et al., APL Materials 4, 126103 (2016).

[7] J. Růžička et al., New J. Phys. 17, 013028 (2015).

[8] K. Carva et al., Phys. Rev. B 93, 214409 (2016).

[9] V. N. Antonov et al., Phys. Rev. B 96, 224434 (2017).

[10] R. Tarasenko et al., Physica B, 481, 262 (2016).

[11] L. He, X. Kou, and K. L. Wang, Phys. Status Solidi RRL 7, 50 (2013).

[12] G. A. Thomas et al., Phys. Rev. B 46, 1553 (1992).

[13] C. S. Fadley, J. Electron Spectrosc. Relat. Phenom. 190, 165 (2013).

[14] V. N. Strocov et al., J. Synchrotron Radiat. 21, 32 (2014).

ⒸJASRI

(Received: March 30, 2018; Early edition: October 30, 2018; Accepted: December 17, 2018; Published: January 25, 2019)